ITensors.jl
ITensor is a library for rapidly creating correct and efficient tensor network algorithms.
| Documentation | Citation |
|---|---|
  |   |
| Version | Download Statistics | Style Guide | License |
|---|---|---|---|
 |  |  |
The source code for ITensors.jl can be found on Github.
Additional documentation can be found on the ITensor website itensor.org.
An ITensor is a tensor whose interface is independent of its memory layout. ITensor indices are objects which carry extra information and which 'recognize' each other (compare equal to each other).
The ITensorMPS.jl library includes composable and extensible algorithms for optimizing and transforming tensor networks, such as matrix product state and matrix product operators, such as the DMRG algorithm. If you are looking for information on running finite MPS/MPO calculations such as DMRG, take a look at the ITensorMPS.jl documentation.
Support


ITensors.jl is supported by the Flatiron Institute, a division of the Simons Foundation.
News
March 26, 2025: ITensors.jl v0.9 has been released. This is a minor breaking change since the
optimal_contraction_sequencefunction now passes to theoptimaltreefunction from TensorOperations.jl. TheTensorOperationspackage therefore needs to be loaded in order foroptimal_contraction_sequenceto be used or if the flagITensors.enable_contraction_sequence_optimization()is switched on.March 22, 2025: As part of the latest release of ITensors.jl (v0.8.3), all documentation related to MPS/MPO functionality has been moved to the ITensorMPS.jl documentation.
February 22, 2025: Please note that there were issues installing the latest version of ITensors.jl (ITensors.jl v0.8) in older versions of Julia v1.10 and v1.11 (https://github.com/ITensor/ITensors.jl/issues/1618, https://itensor.discourse.group/t/typeparameteraccessors-not-found-error-on-julia-v-1-10-0/2260). This issue has been fixed in NDTensors.jl v0.4.4, so please try updating your packages if you are using older versions of Julia v1.10 or v1.11 and running into issues installing ITensors.jl.
February 3, 2025: ITensors.jl v0.8 has been released. This release should not be breaking to the average user using documented features of the library. This removes internal submodules that held experimental code for rewriting the internals of NDTensors.jl/ITensors.jl, which have now been turned into separate packages for future development. It is marked as breaking since ITensorMPS.jl was making use of some of that experimental code, and will be updated accordingly. Also note that it fixes an issue that existed in some more recent versions of NDTensors.jl v0.3/ITensors.jl v0.7 where loading ITensors.jl in combination with some packages like LinearMaps.jl caused very long load/compile times (https://itensor.discourse.group/t/linearmaps-and-itensors-incompatibility/2216), so if you are seeing that issue when using ITensors.jl v0.7 you should upgrade to this version.
October 25, 2024: ITensors.jl v0.7 has been released. This is a major breaking change, since all of the MPS/MPO functionality from this package has been moved to ITensorMPS.jl, along with all of the functionality of ITensorTDVP.jl. If you want to use MPS/MPO types and related functionality, such as
MPS,MPO,dmrg,siteinds,OpSum,op, etc. you now must install and load the ITensorMPS.jl package. Additionally, if you are using ITensorTDVP.jl in your code, please changeusing ITensorTDVPtousing ITensorMPS. ITensorMPS.jl has all of the same functionality as ITensorTDVP.jl, and ITensorTDVP.jl will be deprecated in favor of ITensorMPS.jl. Note: If you are usingITensors.compile, you must now install and load the ITensorMPS.jl package in order to trigger it to load properly, since it relies on running MPS/MPO functionality as example code for Julia to compile.May 9, 2024: A new package ITensorMPS.jl has been released. We plan to move all of the MPS/MPO functionality in ITensors.jl to ITensorMPS.jl. For now, ITensorMPS.jl just re-exports the MPS/MPO functionality of ITensors.jl (as well as of ITensorTDVP.jl), such as
dmrg,siteinds,MPS,MPO, etc. To prepare for the change over to ITensorMPS.jl, please changeusing ITensorstousing ITensors, ITensorMPSin any code that makes use of MPS/MPO functionality, and if you are using ITensorTDVP.jl changeusing ITensorTDVPtousing ITensorMPSin your code.May 8, 2024: ITensors.jl v0.6 has been released. This version deletes the experimental "combine-contract" contraction backend, which was enabled by
ITensors.enable_combine_contract(). This feature enabled performing ITensor contractions by first combining indices and then performing contractions as matrix multiplications, which potentially could lead to speedups for certain contractions involving higher-order QN-conserving tensors. However, the speedups weren't consistent with the current implementation, and this feature will be incorporated into the library in a more systematic way when we release our new non-abelian symmetric tensor backend.May 2, 2024: ITensors.jl v0.5 has been released. This version removes PackageCompiler.jl as a dependency and moves the package compilation functionality into a package extension. In order to use the
ITensors.compile()function going forward, you need to install the PackageCompiler.jl package withusing Pkg: Pkg; Pkg.add("PackageCompiler")and putusing PackageCompilertogether withusing ITensorsin your code.April 16, 2024: ITensors.jl v0.4 has been released. This version removes HDF5.jl as a dependency and moves the HDF5 read and write functions for ITensor, MPS, MPO, and other associated types into a package extension. To enable ITensor HDF5 features, install the HDF5.jl package with
using Pkg: Pkg; Pkg.add("HDF5")and putusing HDF5together withusing ITensorsin your code. Other recent changes include support for multiple GPU backends using package extensions.March 25, 2022: ITensors.jl v0.3 has been released. The main breaking change is that we no longer support versions of Julia below 1.6. Julia 1.6 is the long term support version of Julia (LTS), which means that going forward versions below Julia 1.6 won't be as well supported with bug fixes and improvements. Additionally, Julia 1.6 introduced many improvements including syntax improvements that we would like to start using with ITensors.jl, which becomes challenging if we try to support Julia versions below 1.6. See here and here for some nice summaries of the Julia 1.6 release.
Jun 09, 2021: ITensors.jl v0.2 has been released, with a few breaking changes as well as a variety of bug fixes
and new features. Take a look at the upgrade guide for help upgrading your code.
Installation
The ITensors package can be installed with the Julia package manager. From the Julia REPL, type ] to enter the Pkg REPL mode and run:
~ juliajulia> ]
pkg> add ITensorsOr, equivalently, via the Pkg API:
julia> import Pkg; Pkg.add("ITensors")Please note that right now, ITensors.jl requires that you use Julia v1.3 or later (since ITensors.jl relies on a feature that was introduced in Julia v1.3).
We recommend using ITensors.jl with Intel MKL in order to get the best possible performance. If you have not done so already, you can replace your current BLAS and LAPACK implementation with MKL by using the MKL.jl package. Please follow the instructions here.
Documentation
- LATEST – documentation of the latest version.
Citation
If you use ITensor in your work, please cite the ITensor Paper:
@article{ITensor,
title={{The ITensor Software Library for Tensor Network Calculations}},
author={Matthew Fishman and Steven R. White and E. Miles Stoudenmire},
journal={SciPost Phys. Codebases},
pages={4},
year={2022},
publisher={SciPost},
doi={10.21468/SciPostPhysCodeb.4},
url={https://scipost.org/10.21468/SciPostPhysCodeb.4},
}and associated "Codebase Release" for the version you have used. The current one is
@article{ITensor-r0.3,
title={{Codebase release 0.3 for ITensor}},
author={Matthew Fishman and Steven R. White and E. Miles Stoudenmire},
journal={SciPost Phys. Codebases},
pages={4-r0.3},
year={2022},
publisher={SciPost},
doi={10.21468/SciPostPhysCodeb.4-r0.3},
url={https://scipost.org/10.21468/SciPostPhysCodeb.4-r0.3},
}ITensor Code Samples
Basic Overview
ITensor construction, setting of elements, contraction, and addition. Before constructing an ITensor, one constructs Index objects representing tensor indices.
using ITensors
let
i = Index(3)
j = Index(5)
k = Index(2)
l = Index(7)
A = ITensor(i,j,k)
B = ITensor(j,l)
# Set elements of A
A[i=>1,j=>1,k=>1] = 11.1
A[i=>2,j=>1,k=>2] = -21.2
A[k=>1,i=>3,j=>1] = 31.1 # can provide Index values in any order
# ...
# Contract over shared index j
C = A * B
@show hasinds(C,i,k,l) # = true
D = random_itensor(k,j,i) # ITensor with random elements
# Add two ITensors
# must have same set of indices
# but can be in any order
R = A + D
nothing
end
# output
hasinds(C, i, k, l) = trueSingular Value Decomposition (SVD) of a Matrix
In this example, we create a random 10x20 matrix and compute its SVD. The resulting factors can be simply multiplied back together using the ITensor * operation, which automatically recognizes the matching indices between U and S, and between S and V and contracts (sums over) them.
using ITensors
let
i = Index(10) # index of dimension 10
j = Index(20) # index of dimension 20
M = random_itensor(i,j) # random matrix, indices i,j
U,S,V = svd(M,i) # compute SVD with i as row index
@show M ≈ U*S*V # = true
nothing
end
# output
M ≈ U * S * V = trueSingular Value Decomposition (SVD) of a Tensor
In this example, we create a random 4x4x4x4 tensor and compute its SVD, temporarily treating the indices i and k together as the "row" index and j and l as the "column" index for the purposes of the SVD. The resulting factors can be simply multiplied back together using the ITensor * operation, which automatically recognizes the matching indices between U and S, and between S and V and contracts (sums over) them.
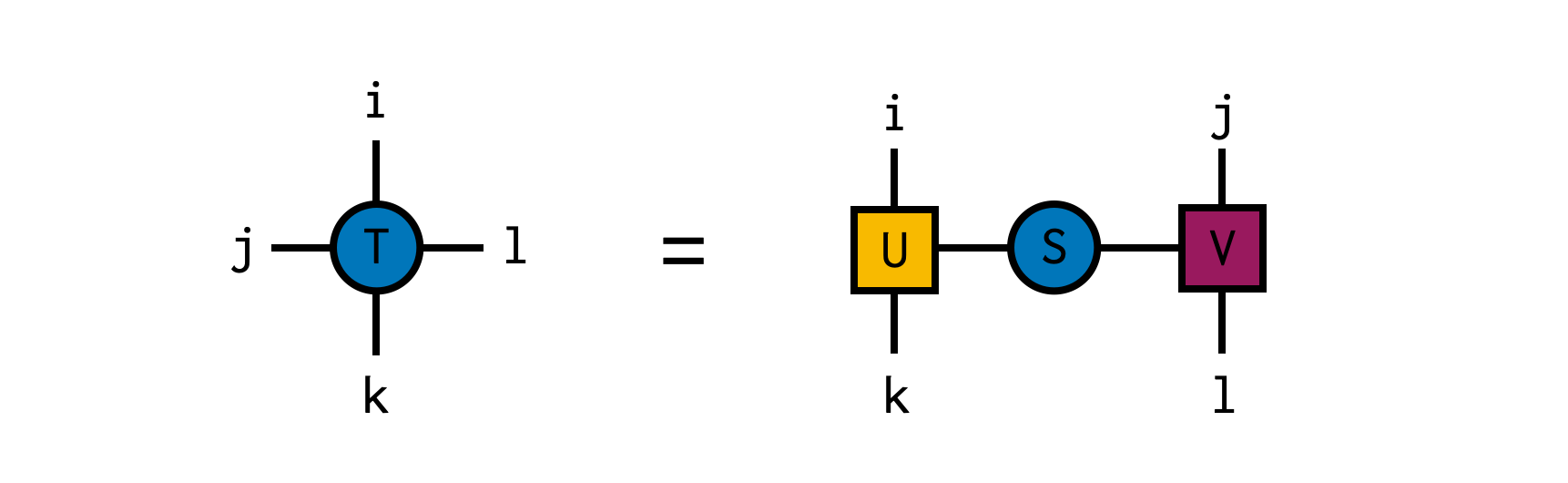
using ITensors
let
i = Index(4,"i")
j = Index(4,"j")
k = Index(4,"k")
l = Index(4,"l")
T = random_itensor(i,j,k,l)
U,S,V = svd(T,i,k) # compute SVD with (i,k) as row indices (indices of U)
@show hasinds(U,i,k) # = true
@show hasinds(V,j,l) # = true
@show T ≈ U*S*V # = true
nothing
end
# output
hasinds(U, i, k) = true
hasinds(V, j, l) = true
T ≈ U * S * V = trueTensor Indices: Tags and Prime Levels
Before making an ITensor, you have to define its indices. Tensor Index objects carry extra information beyond just their dimension.
All Index objects carry a permanent, immutable id number which is determined when it is constructed, and allow it to be matched (compare equal) with copies of itself.
Additionally, an Index can have up to four tag strings, and an integer primelevel. If two Index objects have different tags or different prime levels, they do not compare equal even if they have the same id.
Tags are also useful for identifying Index objects when printing tensors, and for performing certain Index manipulations (e.g. priming indices having certain sets of tags).
using ITensors
let
i = Index(3) # Index of dimension 3
@show dim(i) # = 3
@show id(i) # = 0x5d28aa559dd13001 or similar
ci = copy(i)
@show ci == i # = true
j = Index(5,"j") # Index with a tag "j"
@show j == i # = false
s = Index(2,"n=1,Site") # Index with two tags,
# "Site" and "n=1"
@show hastags(s,"Site") # = true
@show hastags(s,"n=1") # = true
i1 = prime(i) # i1 has a "prime level" of 1
# but otherwise same properties as i
@show i1 == i # = false, prime levels do not match
nothing
end
# output
dim(i) = 3
id(i) = 0x5d28aa559dd13001
ci == i = true
j == i = false
hastags(s, "Site") = true
hastags(s, "n=1") = true
i1 == i = false